|
:: MVP ::
|

|
|
:: RSS ::
|

|
|
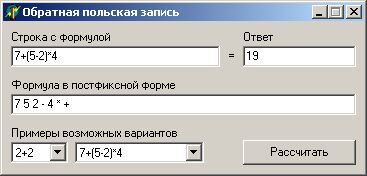
Сегодня нам предстоит разобраться с очень интересной темой, а именно, мы
будем писать программу, которая сможет посчитать строку с формулой.
Для начала немного теории. Форма записи алгебраических выражений, которая
знакома нам со школы, называется инфиксной (infix). Для этой формы записи
характерно то, что знаки операций располагаются между операндами, а в самой
записи могут присутствовать скобки. При построении трансляторов произвольных
алгебраических выражений, заданных в инфиксной форме, возникает ряд сложностей,
а именно:
- Последовательность выполнения операций зависит от скобочной структуры выражения
- Внутри скобок последовательность выполнения операций зависит от их приоритета
От этих сложностей можно избавиться, представив выражение в постфиксной форме
(postfix), которую еще называют обратной польской записью. Выражение в постфиксной
форме не имеет скобок, что позволяет не обращать внимания на приоритеты, связанные
с ними. А за счет того, что все операнды расположены перед знаком операции, выражение
можно вычислить последовательно, за один проход слева направо, что позволяет не
учитывать приоритетов знаков операций.
Посмотрим несколько примеров записи выражения в инфиксной и постфиксной форме.
Инфиксная форма записи Постфиксная форма записи
7 + ( 5 - 2 ) * 4 7 5 2 - 4 * +
8 / ( 2 + 2 ) ^ 2 8 2 2 + 2 ^ /
( 8 / ( 2 + 2 ) ) ^ 2 8 2 2 + / 2 ^
exp( 2 * ln ( 3 ) ) 2 3 ln * exp
|
Если посмотреть внимательно, можно заметить, что операнды в постфиксной
форме не меняют своего относительного расположения, а вот порядок следования
операций и функций меняется как по отношению к операндам, так и по отношению
друг к другу.
А теперь разберем на простом примере алгоритм перевода алгебраического выражения
из инфиксной в постфиксную форму. Пример пусть будет такой: a*(b-c)+d. При
разборе нам понадобится два стека. Первый стек - временный, в него мы будем помещать
знаки операций (далее в тексте я буду называть его временным стеком). А во втором
стеке мы будем формировать выражение в постфиксной форме (далее в тексте - основной
стек). Опишем алгоритм по шагам, разбирая каждый символ.
- Если символ - число (или переменная), помещаем его в основной стек.
- Если символ - знак операции ('+', '-', '/', '*'), то проверяем приоритет
данной операции. Операции умножения и деления имеют наивысший приоритет (3),
операции сложения и вычитания имеют меньший приоритет (2), самый низкий
приоритет (1) имеет открывающая скобка.
- Если временный стек пуст, или находящиеся в нем символы (а находиться
в нем могут только знаки операций и открывающая скобка) имеют меньший
приоритет, чем приоритет текущего символа, то помещаем текущий символ
во временный стек.
- Если символ, находящийся на вершине стека имеет приоритет, больший или
равный приоритету текущего символа, то извлекаем символы из стека в
основной стек до тех пор, пока не встретим символ с меньшим приоритетом.
Встретив символ с меньшим приоритетом, мы прекращаем извлекать символы из
временного стека, и ни в коем случае не забываем добавить во временный
стек текущий символ. Переходим к предыдущему пункту.
- Если символ - открывающая скобка, то помещаем ее во временный стек.
- Если символ - закрывающая скобка, то извлекаем символы из временного стека в
основной до тех пор, пока не встретим во временном стеке открывающую скобку,
которую просто уничтожаем. Закрывающая скобка также уничтожается.
- Если вся входная строка разобрана, но во временном стеке еще остаются знаки операций,
мы должны просто извлечь их в основной стек, начиная с последнего символа.
Разберем наш пример: a*(b-c)+d.
a*(b-c)+d
Текущий символ Основной стек Временный стек
a a пусто
* a *
( a *(
b ab *(
- ab *(-
c abc *(-
) abc- *
+ abc-* +
d abc-*d +
вся разобрана abc-*d+ пусто
|
Теперь посмотрим, как вычислить выражение, записанное в постфиксной форме. Возьмем
наш пример a*(b-c)+d, и заменим операнды числами, например, так: 2*(8-5)+4. В
постфиксной форме это выражение будет выглядеть следующим образом: 285-*4+. И снова
нам нужно два стека. Первый у нас уже есть, это основной стек, в котором находится
выражение в постфиксной форме. Второй стек - стек для расчета (далее в тексте -
расчетный стек). Алгоритм выглядит следующим образом, идем по основному стеку и смотрим:
- Если очередной символ основного стека - число, то кладем его в расчетный стек.
- Если очередной символ основного стека - знак операции, извлекаем из расчетного
стека два верхних числа, используем их в качестве операндов для текущей операции,
затем кладем результат обратно в расчетный стек.
Когда вся входная строка будет разобрана, в расчетном стеке должно остаться одно число,
которое и будет результатом данного выражения. Пример.
285-*4+
Текущий символ Действие Расчетный стек
2 -> 2
8 -> 28
5 -> 285
- 8-5=3 ->3 23
* 2*3=6 ->6 6
4 -> 64
+ 6+4=10 ->10 10
|
Ответ 10.
Как видите, ничего сложного. Теперь рассмотрим реализацию. Не станем сильно мудрить
при написании парсера, и воспользуемся классом TParser. Сейчас я не стану рассказывать
об этом классе (я о нем уже писал), а если вы с ним еще не знакомы и хотите разобраться,
прочтите статью TParser - недокументированный класс для парсинга.
Вот как выглядит процедура разбора строки с формулой.
(* Получение приоритета *)
function GetPriority( c: char ): byte;
begin
Result := 0;
case c of
'(': Result := 1;
'+', '-': Result := 2;
'*', '/': Result := 3;
'^', '!': Result := 4;
'c', 's', 'l', 'e': Result := 5;
'n': Result := 6;
end;
end;
(* Переводим строку с формулой в обратную польскую запись *)
procedure ParseString( s: AnsiString; var _Stack: TStringList );
var
Ms: TMemoryStream;
Temp: TStringList; // Временный стек для знаков и геометрических функций
flag: boolean;
begin
Temp := TStringList.Create;
Ms := TMemoryStream.Create;
Ms.WriteBuffer( s[1], Length( s ) );
Ms.Position := 0;
with TParser.Create( Ms ) do
begin
while Token <> toEof do
begin
// Если это число, помещаем его в выходной стек
if ( TokenString[1] in ['0'..'9'] ) then
if flag then
begin
_Stack[_Stack.Count-1] := _Stack[_Stack.Count-1] + TokenString;
flag := false;
end
else
_Stack.Add( TokenString );
// Если это разделитель дробной части
if ( TokenString[1] in [DecimalSeparator] ) then
begin
_Stack[_Stack.Count-1] := _Stack[_Stack.Count-1] + TokenString;
flag := true;
end;
// Если это знак (или геометрическая функция), то...
if ( TokenString[1] in ['+','-','/','*','^','!','c','s','l','n','e'] ) then
begin
// ...если стек пустой, помещаем знак в стек ...
if Temp.Count = 0 then
Temp.Add( TokenString )
else
begin
// ... если приоритет текущей операции выше, чем приоритет
// последней операции в стеке, помещаем знак в стек ...
if GetPriority( TokenString[1] ) > GetPriority( Temp.Strings[Temp.Count-1][1] ) then
Temp.Add( TokenString )
else
begin
// ... иначе извлекаем из стека все операции, пока
// не встретим операцию с более высшим приоритетом
while true do
begin
_Stack.Add( Temp.Strings[Temp.Count-1] );
Temp.Delete( Temp.Count-1 );
if Temp.Count = 0 then Break;
if GetPriority( TokenString[1] ) > GetPriority( Temp.Strings[Temp.Count-1][1] ) then
Break;
end;
// Не забываем добавить в стек текущую операцию
Temp.Add( TokenString );
end;
end;
end;
// Если это открывающая скобка, помещаем ее в стек операций
if ( TokenString[1] in ['('] ) then
Temp.Add( TokenString );
// Если это закрывающая скобка, извлекаем из стека операций в
// выходной стек все операции, пока не встретим открывающую скобку.
// Сами скобки при этом уничтожаются.
if ( TokenString[1] in [')'] ) then
while true do
begin
if Temp.Count = 0 then Break;
if Temp.Strings[Temp.Count-1] = '(' then
begin
Temp.Delete( Temp.Count-1 );
Break;
end;
_Stack.Add( Temp.Strings[Temp.Count-1] );
Temp.Delete( Temp.Count-1 );
end;
NextToken;
end;
end;
Ms.Free;
// Если по окончании разбора строки с формулой, в стеке операций
// еще чтото осталось, извлекаем все в выходной стек
if Temp.Count <> 0 then
while Temp.Count <> 0 do
begin
_Stack.Add( Temp.Strings[Temp.Count-1] );
Temp.Delete( Temp.Count-1 );
end;
Temp.Free;
end;
|
Мы получили выражение в виде обратной польской записи, а теперь рассчитаем его:
(* Вычисляем факториал *)
function Factorial( ch: integer ): integer;
var
i: integer;
begin
if ch < 0 then
begin
Result := 2147483648; // 2147483647 + 1 - выход за пределы integer
Exit;
end;
Result := 1;
if ch = 0 then
Exit;
for i := 1 to ch do
Result := Result * i;
end;
(* Рассчитываем выражение в постфиксной форме *)
function Calculate( var _Stack: TStringList ): real;
var
i: integer;
a1, a2: real;
Temp: TStringList; // Временный стек для рассчетов
begin
Result := 0;
Temp := TStringList.Create;
for i := 0 to _Stack.Count-1 do
// Если зто число, помещаем его в стек для рассчета, иначе ...
if _Stack.Strings[i][1] in ['0'..'9'] then
Temp.Add( _Stack.Strings[i] )
else
begin
// ... Вынимаем из стека рассчета последнее число
a2 := StrToFloat( Temp.Strings[Temp.Count-1] );
Temp.Delete( Temp.Count-1 );
// если для выполнения операции требуется 2 аргумента,
// вынимаем из стека рассчета еще одно число
if _Stack.Strings[i][1] in ['+','-','/','*','^'] then
begin
a1 := StrToFloat( Temp.Strings[Temp.Count-1] );
Temp.Delete( Temp.Count-1 );
end;
// Производим рассчет
case _Stack.Strings[i][1] of
'+': Temp.Add( FloatToStr( a1 + a2 ) );
'-': Temp.Add( FloatToStr( a1 - a2 ) );
'/': Temp.Add( FloatToStr( a1 / a2 ) );
'*': Temp.Add( FloatToStr( a1 * a2 ) );
'^': Temp.Add( FloatToStr( Power( a1, a2 ) ) );
'!': Temp.Add( FloatToStr( Factorial( Round( a2 ) ) ) );
'c': Temp.Add( FloatToStr( cos( a2 ) ) );
's': Temp.Add( FloatToStr( sin( a2 ) ) );
'l': Temp.Add( FloatToStr( ln( a2 ) ) );
'n': Temp.Add( FloatToStr( -a2 ) );
'e': Temp.Add( FloatToStr( exp( a2 ) ) );
end;
end;
Result := StrToFloat( Temp.Strings[0] );
Temp.Free;
end;
|
Процедура Power (возведение в степень) взята из модуля Math, а функцию для расчета
факториала мы написали сами. В заключение скажу несколько слов о том, что стоит
доработать. Функциональность данного приложения довольно просто расширить (добавить
новые операции, например tg, or, xor, and, mod, div и т.д.), но тут нас ждет небольшая
проблема. Посмотрите, как производится расчет. Используя оператор case, мы
определяем действие, которое нужно выполнить, по первому символу оператора. Очевидно,
что при таком подходе, в программе не должно быть действий, имеющих одинаковый первый
символ (например: ln и log). Есть два пути решения.
- Вместо case использовать if, и проверять не по первому символу,
а по всей строке. Но большое количество if в одном месте программы
сделают код некрасивым и трудно читаемым. Поэтому, я бы порекомендовал
второй способ.
- Перед началом разбора выражения, заменить все операторы, входящие в него,
простыми символами, например: 'sin' меняем на 'a', 'cos'
меняем на 'b', 'tg' меняем на 'c' и т.д. Для подобной замены
можно воспользоваться функцией StringReplace, после чего, мы сможем
работать с этими символами, как с обычными операторами, используя case.
Кроме этого, перед началом разбора, можно сделать проверку на правильность введенных
данных: парное количество скобок, их правильное расположение, а также проверять заведомо
неверные аргументы функций, например ln(-1) [в программе ln(not(1))] или -3!
[в программе not(3)!].
Это все, о чем я хотел рассказать сегодня. Удачи в программировании.
.: Пример к данной статье :.
|
|
При использовании материала - ссылка на сайт обязательна
|
|


