|
:: MVP ::
|

|
|
:: RSS ::
|

|
|
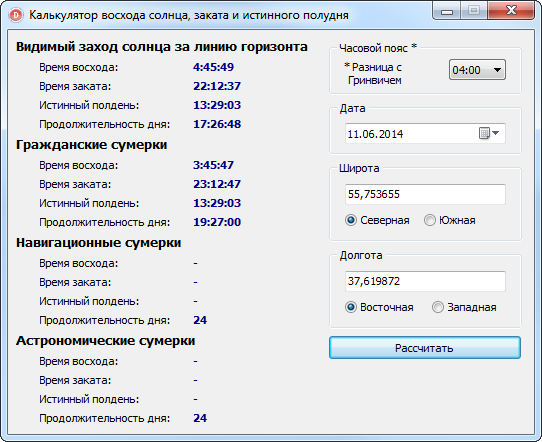
За основу взят алгоритм расчета, который можно посмотреть
здесь.
Источник алгоритма - Almanac for Computers, 1990, published by Nautical Almanac Office,
United States Naval Observatory, Washington, DC 20392. В комментариях к алгоритму также было
указано, что он верен для периода с 1980 по 2050 год, и обладает точностью до одной минуты.
Однако точность уменьшается для мест, лежащих на широтах выше 60 градусов северной или южной
широты. Выше 80 градусов погрешности в расчете эклиптики (плоскость вращения Земли вокруг Солнца)
приводят к еще большим ошибкам (каким - не сказано).
Перевод этого алгоритма на Delphi выглядит следующим образом:
function GetSunTime( const Dt: TDate; const Latitude, Longitude, Zenith: Extended;
const LocalOffset: Byte; const SunTime: TSunTime ): TTime;
var
N: Word;
LngHour, M, L, RA, Lquadrant, RAquadrant,
sinDec, cosDec, HCos, H, LocalT, UT: Double;
t: TTime;
begin
// 1. first calculate the day of the year
N := Trunc( GetDays( Dt ) );
// ----------
// 2. convert the longitude to hour value and calculate an approximate time
LngHour := Longitude / 15;
// if rising time is desired:
// t := N + ( ( 6 - LngHour ) / 24 );
// if setting time is desired:
// t := N + ( ( 18 - LngHour ) / 24 );
case SunTime of
Sunrise: t := N + ( ( 6 - LngHour ) / 24 );
Sunset: t := N + ( ( 18 - LngHour ) / 24 );
end;
// ----------
// 3. calculate the Sun's mean anomaly
M := ( 0.9856 * t ) - 3.289;
// ----------
// 4. calculate the Sun's true longitude
// [Note throughout the arguments of the trig functions
// (sin, tan) are in degrees. It will likely be necessary to
// convert to radians. eg sin(170.626 deg) =sin(170.626*pi/180
// radians)=0.16287]
L := M + ( 1.916 * Sin( DegToRad( M ) ) ) +
( 0.020 * Sin( DegToRad( 2 * M ) ) ) + 282.634;
// NOTE: L potentially needs to be adjusted into the range [0,360) by adding/subtracting 360
Adjust( L, 360 );
// ----------
// 5a. calculate the Sun's right ascension
RA := RadToDeg( ArcTan( 0.91764 * Tan( DegToRad( L ) ) ) );
// NOTE: RA potentially needs to be adjusted into the range [0,360) by adding/subtracting 360
Adjust( RA, 360 );
// ----------
// 5b. right ascension value needs to be in the same quadrant as L
Lquadrant := Floor( L / 90 ) * 90;
RAquadrant := Floor( RA / 90 ) * 90;
RA := RA + ( Lquadrant - RAquadrant );
// ----------
// 5c. right ascension value needs to be converted into hours
RA := RA / 15;
// ----------
// 6. calculate the Sun's declination
sinDec := 0.39782 * Sin( DegToRad( L ) );
cosDec := Cos( ArcSin( sinDec ) );
// ----------
// 7a. calculate the Sun's local hour angle
HCos := ( Cos( DegToRad( Zenith ) ) - ( sinDec * Sin( DegToRad( Latitude ) ) ) ) /
( cosDec * Cos( DegToRad( Latitude ) ) );
// if (cosH > 1)
// the sun never rises on this location (on the specified date)
// if (cosH < -1)
// the sun never sets on this location (on the specified date)
if ( HCos > 1 ) or ( HCos < -1 ) then
Exit;
// ----------
// 7b. finish calculating H and convert into hours
// if rising time is desired:
// H := 360 - RadToDeg( ArcCos( HCos ) );
// if setting time is desired:
// H := RadToDeg( ArcCos( HCos ) );
case SunTime of
Sunrise: H := 360 - RadToDeg( ArcCos( HCos ) );
Sunset: H := RadToDeg( ArcCos( HCos ) );
end;
H := H / 15;
// ----------
// 8. calculate local mean time of rising/setting
LocalT := H + RA - ( 0.06571 * t ) - 6.622;
// ----------
// 9. adjust back to UTC
UT := LocalT - LngHour;
// NOTE: UT potentially needs to be adjusted into the range [0,24) by adding/subtracting 24
Adjust( UT, 24 );
// ----------
// 10. convert UT value to local time zone of latitude/longitude
Result := UT + LocalOffset;
Adjust( Double( Result ), 24 );
end;
|
Входные параметры функции:
Dt – дата, для которой рассчитывается время;
Latitude – географическая широта места, для которого производится расчет;
Longitude – географическая долгота места, для которого производится расчет;
Zenith – угол солнца (подробнее об этом ниже);
LocalOffset – часовой пояс (разница с Гринвичем);
SunTime – параметр, определяющий искомую величину – время восхода или заката.
Нюанс – на высоких широтах зимой и летом солнце может либо никогда не заходить
(полярный день) либо никогда не восходить (полярная ночь). Это надо учитывать.
Приведенная выше функция в таких случаях в качестве результата возвращает
продолжительность дня 24 часа полярного для, либо 0 часов для полярной ночи.
Зенитный угол, который определяет границу дня/ночи, оказывает существенное влияние
на расчет. Зенит – линия, направленная из точки на поверхности земли вертикально вверх,
а зенитный угол – это угол между вертикалью и направлением на центр небесного объекта.
В данном случае речь идет о том, какой величины должен быть этот угол, чтобы считать,
что солнце уже "совсем" взошло или уже село и день сменился ночью или наоборот.
Если бы Солнце было точкой, а Земля не имела атмосферы, то зенитный угол, определяющий
полный закат солнца, был бы равен 90 градусам. Но поскольку Солнце не точка, и имеет
угловой диаметр, а его свет отражается твердыми частицами в атмосфере, то для того,
чтобы верхний край солнечного диска скрылся за горизонтом, его центр должен лежать уже
чуть ниже горизонта. При нормальных атмосферных условиях это соответствует углу в 90
градусов 50 минут. Этот угол считается углом "официального" заката солнца.
Но хотя солнце и скрылось за горизонтом, за счет отражения его света от атмосферы все еще
довольно светло. Начинается период времени, называемый сумерками. Сумерки делятся на три
этапа – гражданские, навигационные и астрономические (в зависимости от угла погружения
Солнца под горизонт), и конец каждого из этапов тоже можно взять за точку заката солнца.
Первый этап называется гражданскими сумерками. Гражданские сумерки — наиболее светлая часть
сумерек, длящаяся от момента видимого захода Солнца за линию горизонта до момента погружения
центра Солнца под линию горизонта на 6 градусов (гражданские сумерки заканчиваются вечером и
начинаются утром, когда центр солнечного диска находится на высоте 6 градусов ниже горизонта).
Этот фактор учитывается в некоторых законах, таких как обязательное включение фар после захода
Солнца или рассмотрение грабежа в это время как ночной грабёж, который в некоторых уголовных
кодексах наказывается строже. В этот период (при хороших атмосферных условиях освещения) еще
достаточно светло, чтобы работать вне помещения без искусственного освещения и чётко видеть
наземные объекты. Концу гражданских сумерек соответствует зенитный угол в 96 градусов, после
чего начинаются навигационные сумерки.
Навигационные сумерки – достаточно светлая часть сумерек, когда центр Солнца находится ниже
горизонта от 6,01 до 12 градусов. Считается, что в эту часть сумерек уже хорошо видны все
навигационные звезды и, всё еще видна линия горизонта, что позволяет судоводителю использовать
секстант для измерения угла между небесными светилами и видимым горизонтом. Тем не менее, такого
освещения недостаточно для нормальной жизнедеятельности человека (освещение на улице ближе к
ночному, чем к вечернему в классическом понимании), поэтому улицы населённых пунктов нуждаются
в искусственном освещении. Концу навигационных сумерек соответствует зенитный угол в 102 градуса,
после чего начинаются астрономические сумерки.
Астрономические сумерки - время, когда Солнце находится от 12,01 до 18 градусов ниже горизонта.
В это время, когда Солнце все еще является источником света и мешает видимости самых слабых звезд.
Для обычного наблюдателя это время неотличимо от ночи. Концу астрономических сумерек соответствует
момент, когда Солнце полностью прекращает быть источником света, и это зенитный угол в 108 градусов.
Еще один нюанс – алгоритм выдает результат в гринвичском времени, но для большего удобства
пользователя надо перевести это время в местное. В идеальном мире часовой пояс можно было бы
получить, используя значение долготы места. В самом деле, земной сфероид делится на 24 сферических
двуугольника, по меридианам, отстоящим друг от друга на 15 градусов, и часовой пояс вычисляется
тривиально. Но в реальном мире все не так – политические, административные и географические
границы придали весьма забавную форму часовым поясам, так что определение пояса по долготе не
представляется возможным. Поэтому процедура имеет дополнительный параметр для указания смещения
относительно гринвичского времени, это самый простой и быстрый путь решения данной проблемы.
С расчётом истинного времени все гораздо проще. Если учесть значение уравнения времени (разница
между средним солнечным временем и истинным солнечным временем), то можно узнать истинное время
на основании точного гражданского времени В общем виде формула очень проста. Если ST — истинное время,
а UTC — универсальное время по Гринвичу, то формула будет выглядеть так:
ST = UTC + долгота в часовых единицах + EOT (значение уравнения времени)
|
Подробности использования функции GetSunTime Вы найдете в прилагаемом примере.
На этом все, удачного вам программирования!
.: Пример к данной статье :.
|
|
При использовании материала - ссылка на сайт обязательна
|
|


